Do leta 2019 je bila močno uveljavljena hipoteza, da lahko elektroni v kristalu, ob prisotnosti interakcij in dovolj velikega nereda na kristalni mreži, ostanejo ujeti v okolici posameznih mest kristalne mreže. Če imamo v mislih zgolj en elektron, temu pojavu rečemo lokalizacija, če pa imamo v mislih kolektivno stanje množice elektronov, temu rečemo mnogodelčna lokalizacija (angl. many-body localization oziroma MBL). Slednja med drugim napove, da kristal zaradi lokaliziranosti nosilcev naboja ne prevaja električnega toka pri katerikoli temperaturi, in se torej obnaša kot idealni izolator. Rezultati slovenskih raziskovalcev v zadnjih dveh letih postavljajo obstoj te lastnosti pod vprašaj. Vse več je indicev, da je obstoj idealnega izolatorja – in s tem mnogodelčne lokalizacije – ponovno odprt raziskovalni problem.

Že od osnovne šole dalje otroke učimo, da lahko snovi glede na električne prevodne lastnosti razdelimo na prevodnike in izolatorje. Pri tem se po navadi ne poudari, da je prevodnost izolatorjev ničelna le pri temperaturi absolutne ničle (ki ustreza –273 ⁰C). Z drugimi besedami: pri vseh temperaturah nad absolutno ničlo tudi izolator prevaja električni tok, le da je ta bistveno manjši kot tisti v prevodniku. Ob zavedanju teh dilem je bilo zelo osvežujoče spoznanje ameriškega fizika Philipa W. Andersona iz leta 1958. Zanimalo ga je obnašanje elektrona na kristalni mreži ob prisotnosti nereda oziroma neurejenosti na kristalni mreži, ki je denimo posledica naključno spreminjajočega se električnega ali magnetnega polja zaradi nečistoč. Ugotovil je, da lahko elektron ostane ujet na določenem delu mreže, torej da tvori prostorsko lokalizirano stanje. Ta pojav, kasneje poimenovan Andersonova lokalizacija, predstavlja fundamentalno nov fizikalni pojav. Med drugim napove možnost, da elektron zaradi lokaliziranosti ne more prispevati k prevajanju električnega toka. To se lahko zgodi pri poljubno visoki temperaturi in torej odpira vrata obstoju idealnega izolatorja pri sobni temperaturi. Teoretično odkritje tega pojava, katerega obstoj je bil kasneje tudi matematično dokazan, je poželo veliko zanimanja v širši znanstveni skupnosti in P. W. Anderson je bil, skupaj s kolegoma N. Mottom in J. van Vleckom, za svoje dosežke leta 1977 nagrajen z Nobelovo nagrado za fiziko.

Čeprav je teorija Andersonove lokalizacije že sama po sebi dovolj zapletena in zanimiva, ima pri opisu dejanskih eksperimentalnih sistemov ključno pomanjkljivost: ne vključuje vloge meddelčnih interakcij, ki so v realnih materialih tako rekoč vselej prisotne. Iskanje odgovora na vprašanje o tem, ali lokalizirana stanja »preživijo« tudi v prisotnosti meddelčnih interakcij, nikakor ni enostavno. Kljub nekaterim poskusom zaenkrat ne obstaja široko sprejet matematični dokaz o obstoju lokalizacije v prisotnosti meddelčnih interakcij. Zapletenost študij fizikalnih sistemov ob prisotnosti interakcij in nereda morda najbolje ponazori Andersonov komentar ob prejemu Nobelove nagrade, da se moramo za iskanje odgovorov na celo najpreprostejša vprašanja nasloniti na numerične simulacije (oziroma, kot je izvorno zapisal Anderson, "…one has to resort to the indignity of numerical simulations to settle even the simplest questions about it"). Zaradi tega so se raziskovalci resneje lotili študij Andersonove lokalizacije v prisotnosti meddelčnih interakcij šele v zadnjih 15 letih, ko se je zmogljivost in dostopnost računalniških gruč za izvedbo zahtevnih numeričnih simulacij bistveno povečala. Po več kot desetletju intenzivnih raziskav, ki so bile opisane v več kot tisoč znanstvenih objavah, se je zdel odgovor pritrdilen: tudi v prisotnosti interakcij naj bi Andersonova lokalizacija »preživela« in vodila do novega stanja snovi, ki se imenuje mnogodelčna lokalizacija.

Bistvena lastnost morebitnega pojava mnogodelčne lokalizacije je odsotnost termalizacije. To je lastnost, ki je prisotna pri skoraj vseh snoveh v naravi, in jo zato človek ponotranji že v mladih letih. Predstavljajmo si denimo, da v dobro prezračeni sobi razpršimo nek zelo dišeč parfum. To stanje je vsekakor zelo daleč stran od ravnovesnega stanja. Na začetku bo ta soba sicer precej prijetno dišala, a po dolgem času bo vonj zbledel, saj se bodo gradniki plina, ki poskrbijo za odišavljenost, enakomerno porazdelili po vsem dostopnem prostoru, ki je bistveno večji od te sobe. Začetnemu stanju takega eksperimenta bi lahko rekli tudi vzbujeno stanje, rezultatu po dolgem času pa vrnitev nazaj v ravnovesje oziroma termalizacija. V fiziki z izrazom ergodičnost označujemo pojav, ko lastnosti snovi po dolgem času postajajo enake njihovim termalnim lastnostim.

Če bi bil sistem v stanju mnogodelčne lokalizacije, bi bil torej neergodičen in posledično ne bi termaliziral tudi po izjemno dolgih časih. Iz tega bi sledilo kar nekaj izjemno zanimivih lastnosti. Prva lastnost je, da temu stanju ne bi mogli smiselno določiti temperature. Druga lastnost je, da bi se informacija o začetnem stanju po vzbuditvi lahko ohranila za vse čase. V primeru dišečega parfuma bi to pomenilo, da odišavljenost sobe ne bi zbledela s časom, v primeru neergodičnega materiala pa, da bi lahko shranil kvantno informacijo, kar bi ga naredilo zelo zanimivega za morebitne nove tehnološke naprave. Tretja lastnost se navezuje na pričakovanje, da bi do pojava mnogodelčne lokalizacije prišlo pri zadosti velikem neredu na kristalni mreži, medtem ko bi se pri manjših vrednostih nereda sistem obnašal bolj konvencionalno, torej ergodično. To bi pomenilo, da bi s povečevanjem nereda moral obstajati fazni prehod iz ergodičnega stanja snovi v neergodično stanje. Te vrste fazni prehod ne spada v okvire faznih prehodov, ki jih do sedaj poznamo v naravi.

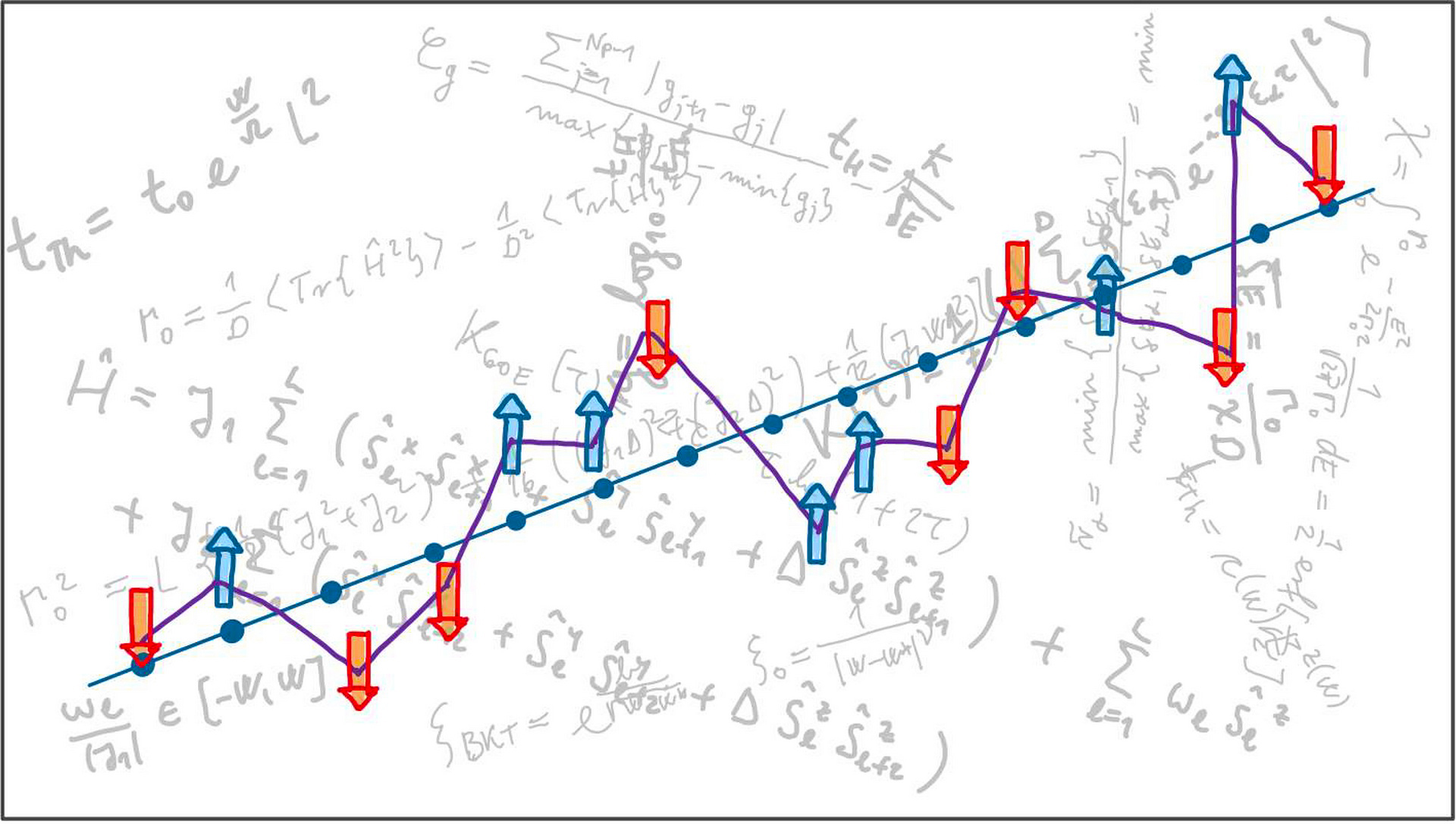
Razumljivo je, da je možnost realizacije teh zanimivih lastnosti snovi pritegnila pozornost velikega števila raziskovalcev. Večina raziskovalcev se je problema lotila bodisi z intenzivnimi numeričnimi simulacijami ali pa z eksperimentalnimi pristopi. Oba pristopa sicer izkazujeta nemalo praktičnih omejitev, saj so recimo točne numerične metode omejene na opis sistemov z majhnim številom mest na kristalni mreži, moderni eksperimenti  pa so omejeni na relativno kratke časovne intervale po vzbuditvi sistema. Do maja 2019 je sicer prevladovalo stališče, da so glavne lastnosti prehoda v mnogodelčno lokalizacijo že precej dobro razvozlane. To stališče je skladno s predpostavko, da fazni prehod med ergodično in neergodično fazo zares obstaja. Vpeljan je bil tudi vzorčni modelski sistem, ki opiše iskano obnašanje: to je veriga delcev z lokalno interakcijo, kjer vsak spin delca, kot je skicirano na zgornji sliki, čuti magnetno polje z naključno vrednostjo. Delce lahko predstavljajo bodisi atomi ali pa elektroni, spin pa je njihova kvantnomehanska lastnost, ki jo lahko vidimo kot neke vrste vrtilno količino.

Maja 2019 pa je bilo na spletnem potralu arXiv.org objavljeno delo slovenskih raziskovalcev z Instituta "Jožef Stefan" in Fakultete za matematiko in fiziko Univerze v Ljubljani, ki je precej zamajalo do takrat prevladujoč pogled na mnogodelčno lokalizacijo. V njem avtorji uporabijo numerična orodja, ki so komplementarna glede na do takrat uporabljena orodja, ter z natančno analizo pridobljenih podatkov zaključijo, da točni numerični računi v okviru sistemov, ki jih lahko obravnavajo današnje največje računalniške gruče, ne kažejo znakov o faznem prehodu med ergodičnim in neergodičnim stanjem. Poleg avtorja tega besedila so bili soavtorji članka, ki je bilo po prvotni objavi na spletnem portal arXiv.org kasneje objavljeno v reviji Physical Review E 102, še Jan Šuntajs, Janez Bonča in Tomaž Prosen.

Lahko si predstavljamo, da ima usoda takega raziskovalnega dela samo dve možnosti: ali se rezultati na dolgi rok izkažejo kot pomanjkljivi, zaradi česar hitro potonejo v pozabo, ali pa spremenijo tok raziskovanja. Kmalu po izvirni objavi se je pojavilo veliko pobud v smeri prve možnosti. Te pobude so bile na začetku dominantne. Zanimivo je bilo pri tem opažanje, da so denimo tisti redki zagovorniki druge možnosti na eni prvih znanstvenih konferenc po maju 2019, ki se je odvijala v Firencah v Italiji, o tem govorili večinoma le šepetaje. Ob tem bi se lahko z malo zgodovinske domišljije spomnili na znanega prebivalca Firenc izpred nekaj stoletij, slavnega fizika Galilea Galilea, ki je po pogromu nad svojim heliocentričnim modelom vesolja in cerkveni inkviziciji le potihoma govoril o gibanju Zemlje »… in vendar se vrti«. Kdo ve – če bi Galileo živel danes, bi o mnogodelčni lokalizaciji morda zašepetal »… in vendar prevaja«, če bi imel v mislih njeno zmožnost prevajanja električnega toka, ali pa »… in vendar termalizira« za njene termodinamske lastnosti.

Vseeno pa se v današnji znanstveni skupnosti dogodki odvijajo precej hitreje kot včasih, ko je moralo miniti nekaj stoletij, da je Galileo Galilei doživel celovito znanstveno rehabilitacijo. Navsezadnje je ravno živahna izmenjava idej znotraj znanstvene skupnosti tisto osnovno gonilo napredka in novih spoznanj, kar so dobri raziskovalci zmeraj znali ceniti. Nedolgo po prvi objavi rezultatov slovenskih raziskovalcev so sledile teoretične objave nekaterih uveljavljenih raziskovalcev iz Severne Amerike in Evrope, ki so pritrjevale tem rezultatom. Poleg tega je nekaj neodvisnih skupin raziskovalcev natančno preverilo numerične rezultate slovenskih raziskovalcev, ki so se vsi izkazali kot verodostojni. Po dobrih dveh letih raziskav je tako postalo precej široko sprejeto stališče, da se morebitni prehod med ergodično in neergodično fazo v spinskih verigah z neredom ne nahaja pri tistih vrednostih nereda, pri katerih se je do maja 2019 verjelo, da se nahaja. Dejanska usoda morebitnega prehoda, in s tem obstoj mnogodelčne lokalizacije, pa je načeloma zopet postala odprt problem. Nekateri danes denimo menijo, da je treba točko prehoda v mnogodelčno lokalizacijo zgolj prestaviti k še višjim vrednostim nereda na kristalni mreži. Drugi menijo, da morda točke prehoda v bližnji in srednjeročni prihodnosti ne bomo našli, četudi skoraj gotovo obstaja. Tretji menijo, da faznega prehoda med ergodično in neergodično fazo snovi, vsaj kar se tiče modelov spinskih verig ob prisotnosti nereda, v resnici ni. Skratka, zopet smo na začetku poti, ki obeta zelo vznemirljiv potek raziskav v naslednjih letih, vključno s postavitvijo novih hipotez. Za celovito ovrednotenje koncepta Andersonove lokalizacije, nagrajenega z Nobelovo nagrado za fiziko leta 1977, še posebno v luči njegove uporabe v realnih materialih in kvantnih simulatorjih, pa bo verjetno treba počakati še vsaj kakšno desetletje. Kot so nedavno ugotovili udeleženci simpozija z naslovom MBL 2021 : Dead or alive?, ki ga je organiziral eden od pionirjev mnogodelčne lokalizacije, je potrebno za celovito razlago koncepta idealnega izolatorja in mnogodelčne lokalizacije vpeljati nove metodološke pristope, ki bodo zelo verjetno v prihodnosti vodili do novih spoznanj ter precej spremenili naše trenutno razumevanje te tematike.