Vedno več se govori o kvantnih računalnikih – računskih strojih, ki so trenutno uporabni predvsem za učinkovito simulacijo kvantnih materialov, v prihodnosti pa naj bi klasične računalnike prehiteli tudi v reševanju bolj vsakdanjih problemov. Med njimi se pogosto omenja logistične probleme (kot je npr. optimizacija tovornega prometa), simulacije molekularne dinamike, ki bi omogočile razvoj novih zdravil, optimizacija finančnih trgov ter šifriranje in dešifriranje sporočil. Redkokdaj pa zasledimo razlago konkretnih problemov, pri reševanju katerih kvantni računalniki prekašajo klasične. To jim omogoča lastnost, ki ji pravimo kvantna prepletenost (angl. quantum entanglement). Po kratkem uvodu v kvantno prepletenost si bomo ogledali igro kvantni magični kvadrat, v kateri se klasično ne da zmagati s stoodstotno verjetnostjo, obstaja pa kvantna strategija, ki to omogoča. Na koncu pa bomo omenili še zanimiv pojav, ki bi lahko močno poenostavil zapleteno pripravo prepletenih kvantnih delcev.
Kvantna prepletenost
Kvantna prepletenost označuje nenavadno soodvisnost lastnosti oddaljenih delcev, ki se je ne da pojasniti s klasično intuicijo. Prepletena delca sta lahko zelo daleč narazen, pa bo meritev kvantnih lastnosti enega izmed njiju popolnoma določila rezultate meritev na drugem, ne glede na to, ali so bile njune lastnosti prej določene ali ne. Pri tem ni pomembno niti, kako hitro ena za drugo sta izvedeni meritvi na posameznih delcih. Izvedemo ju lahko tako hitro zapored, da v vmesnem času niti svetloba (ali informacija) ne more prepotovati razdalje med delcema. Na prvi pogled se to zdi paradoksalno: videti je, kot da meritev na enem delcu v trenutku vpliva na drugega, ne glede na to, kako daleč sta. To je pri nekaterih fizikih, med katerimi so bili Albert Einstein, Boris Podolsky in Nathan Rosen, v začetku 20. stoletja vzbujalo dvome o celovitosti kvantnega opisa narave – Albert Einstein je nelokalne posledice kvantne meritve celo opredelil kot »srhljiv vpliv na daljavo« (angl. spooky action at a distance). Šele več kot trideset let kasneje so kvantno prepletenost tudi eksperimentalno potrdili – za to je bila leta 2022 podeljena Nobelova nagrada za fiziko. Več o zgodovini te »borbe za prepletenost« si lahko preberete v prispevku Roka Žitka, objavljenem prav na tem spletišču. Mi pa se bomo posvetili vprašanju, ali lahko nenavaden pojav kvantne prepletenosti izkoristimo za reševanje problemov, ki jih klasični računalniki ne zmorejo rešiti. To je osnovna ideja kvantne prednosti (angl. quantum advantage) – zmožnosti kvantnih računalnikov, da v nekaterih računskih procesih prehitijo klasične.
V nadaljevanju si bomo natančneje ogledali razmeroma enostaven primer kvantne prednosti. Gre za igro, v kateri morajo soigralci usklajeno odgovarjati na vprašanja, pri tem pa med seboj ne morejo komunicirati. Svoje odgovore lahko uskladijo, če jih izberejo na podlagi rezultatov kvantnih meritev na prepletenih stanjih, ki si jih delijo. Ker meritev prepletenega stanja določi rezultate ostalih meritev, bo odgovor enega izmed soigralcev vedno usklajen z drugimi.
Igra magični kvadrat in zmaga z uporabo prepletenih stanj
Ponazorimo idejo kvantne prednosti, ki jo omogoča prepletenost, na akademskem primeru – igri kvantni magični kvadrat. V zgodnjih devetdesetih letih sta si jo zamislila fizika David Mermin in Asher Peres. V igri proti sodniku igrata namišljena opazovalca Anja in Blaž (v izvirniku morda komu bolj poznana kot Alice in Bob). Sodnik naključno izbere vrstico v 3 × 3 tabeli ter Anji naroči, naj jo zapolni s številoma +1 in –1 tako, da je produkt vseh treh števil –1. Sodnik izbere tudi naključni stolpec, ki ga mora zapolniti Blaž, toda v njegovem primeru mora biti produkt števil +1. Anja in Blaž zmagata, če sta na presečišče vrstice in stolpca postavila isto številko.
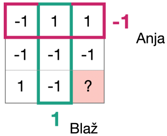
Slika 1: Magični kvadrat. Anja mora v naključno izbrano vrstico –1 postaviti lihokrat, Blaž pa v naključno izbrani stolpec sodokrat. Skupaj lahko zapolnita le osem od devetih kvadratkov – glede zadnjega se ne bosta nikoli strinjala.
Ker med igro ne smeta izmenjevati informacij, je klasična strategija, ki vodi do največjega možnega števila zmag, ta, da se Anja in Blaž vnaprej dogovorita glede vrednosti, ki jih bosta vstavljala. Na ta način se bodo njune vrednosti na presečiščih vedno ujemale. Najti morata torej skupno 3 × 3 tabelo, zapolnjeno s števili +1 in –1 tako, da je zmnožek števil v katerikoli vrstici –1, v kateremkoli stolpcu pa +1. To pa je nemogoče. Blaž, ki polni stolpce, namreč potrebuje vsega skupaj devet števil +1 ali –1, ki se zmnožijo v +1; med njimi torej –1 nastopa sodokrat. Anja, ki polni vrstice, pa potrebuje devet števil +1 ali –1, ki se zmnožijo v –1; med njimi –1 nastopa lihokrat. Tabela, v kateri bi vrednost –1 nastopala lihokrat in sodokrat hkrati, pa ne obstaja. V najboljšem primeru lahko Anja in Blaž skupaj določita samo osem od devetih kvadratkov tabele. O tem, kako zapolniti deveti kvadratek v tabeli, se ne bosta nikoli strinjala – primer tega je prikazan na Sliki 1. Klasično lahko zmagata največ v osmih devetinah vseh ponovitev, torej z verjetnostjo okoli 89 %.
Obstaja pa kvantna strategija, s katero lahko Anja in Blaž zmagata v vsaki ponovitvi igre. Recimo, da Anja in Blaž izvajata meritve na kvantnih stanjih, katerih rezultat je bodisi +1 ali –1. Naključni rezultat meritve je odgovor, ki ga zapišeta na dano mesto v svoji vrstici oziroma stolpcu. V kvantni strategiji Anja in Blaž namesto skupne 3 × 3 tabele odgovorov izbereta skupno 3 × 3 tabelo meritev, ki jih bosta izvedla na kvantnih stanjih. Meritve so izbrane tako, da se njihovi rezultati v vrsticah vedno zmnožijo v –1, v stolpcih pa v +1, ne glede na to, kakšni so na posameznem mestu v vrstici ali stolpcu. Taka skupna tabela meritev obstaja, saj rezultati meritev niso vnaprej določeni. To je bistvena razlika v primerjavi s klasično strategijo – tam so bili lahko odgovori kvečjemu vnaprej pripravljeni, skupna tabela vnaprej pripravljenih odgovorov pa ne obstaja.
Še vedno pa ostane težava, da morata na presečišču vrstice in stolpca Anja in Blaž podati isti odgovor, torej izmeriti isto vrednost. Ta problem rešita tako, da za kvantna stanja, na katerih izvajata meritve, vzameta prepletena stanja. Ko Anja izmeri svoj del prepletenega stanja, dobljeno vrednost zapiše v tabelo. Ker pa je stanje prepleteno, s tem določi tudi vrednost, ki jo bo izmeril in zapisal Blaž. V kvantni strategiji torej Anja in Blaž nedovoljeno izmenjavo informacije o tem, kakšen odgovor je podal kateri izmed njiju, nadomestita s kvantnimi soodvisnostmi, ki določijo rezultat Blaževe meritve glede na to, kaj je izmerila Anja, in obratno. Na ta način lahko v igri zmagata s stoodstotno verjetnostjo.
Od dveh prepletenih delcev do večdelčnih prepletenih stanj
Ugotovitve iz zgornjega primera lahko posplošimo na tabele 4 × 4, 5 × 5, 6 × 6 in tako naprej. Težavnost igre pri tem sicer narašča, vendar lahko v njej s pomočjo kvantnih meritev na prepletenih stanjih še vedno zmagamo s stoodstotno verjetnostjo. Dolgoročni cilj raziskav v kvantnem računalništvu je računski stroj, ki bi bil zmožen zelo težke probleme rešiti veliko hitreje od klasičnih procesorjev. Govorimo o problemih, v katerih nastopa veliko število spremenljivk (npr. tabela n × n, kjer je n zelo veliko število). Uporaben primer je razcep ogromnih števil na praštevila, ki je pomemben v šifriranju sporočil. Naj navedemo, da imajo števila, ki se danes uporabljajo za šifriranje, dolžino okoli 600 desetiških števk. Po nekaterih ocenah bi najmočnejši klasični računalnik za njihov razcep potreboval približno milijardo let. V naslednjih nekaj desetletjih pa bi že lahko imeli kvantne računalnike, ki bi to lahko izvedli v nekaj urah.
Kompleksni problemi z velikim številom spremenljivk zahtevajo pripravo prepletenih stanj velikega števila delcev. To je zahtevna naloga, saj so kvantni pojavi običajno zelo nestabilni. Že najmanjša motnja iz okolice lahko vodi do izgube želenih kvantnih lastnosti, pri velikem številu delcev pa je motnje tudi težje preprečiti. Priprava prepletenih stanj velikega števila delcev je zato zelo zapletena; zahteva zaporedje natančno izvedenih kvantnih meritev in poteka v okolju, ki je dobro izolirano od okolice. Ali jo lahko kako poenostavimo? Ali na primer obstajajo kvantni sistemi, v katerih prepletenost mnogih delcev nastane spontano, kot posledica fizikalnega pojava, ne pa zaradi pametno izbranih operacij s kvantnimi delci?
Spontani razvoj večdelčnih prepletenih stanj
Fizikalni sistemi, v katerih se večdelčna prepletena stanja razvijejo sama od sebe, so redki. Večina fizikalnih sistemov se segreje ali ohladi na temperaturo okolice, pri čemer se soodvisnost zelo oddaljenih delcev izgubi. Taka stanja se močno razlikujejo od prepletenih stanj, ki jih potrebujemo za kvantne računalnike. Če želimo najti kvantni pojav, ki vodi v večdelčno prepleteno stanje, v katerem imajo oddaljeni delci soodvisne lastnosti, moramo iskati med fizikalnimi sistemi, ki se ne ustalijo pri določeni temperaturi. V osemdesetih letih prejšnjega stoletja sta si zanimiv primer takih sistemov skupaj s sodelavci zamislila fizika Richard Palmer in Glenn Fredrickson. Amorfne materiale, kot so stekla, so želeli opisati kot zelo goste tekočine, ki prenehajo teči, ko razdalje med delci postanejo premajhne. Tedaj pride do zastoja delcev, saj ni dovolj prostora, da bi se delci med seboj prerazporedili – potegnemo lahko vzporednice z veliko gnečo na športnem dogodku ali pa z zastojem avtomobilov na avtocesti. Za preučevanje stekel in drugih amorfnih snovi so fiziki razvili preproste modele, ki jim pravimo modeli s kinetičnimi vezmi. Kinetična vez pomeni, da je gibanje delcev močno pogojeno z oddaljenostjo od sosednjih delcev.
Izkaže se, da nekateri takšni sistemi v kvantni fiziki omogočajo spontan razvoj večdelčne prepletenosti. Pred kratkim smo s sodelavci v enem izmed njih odkrili presenetljiv pojav: ko so delci ujeti v zastoju, lahko meritev kvantnih lastnosti le enega izmed njih sproži dramatično spremembo kvantnega stanja. Gre za neke vrste metuljev učinek, saj ima majhna motnja v začetnem stanju dramatične posledice za nadaljnji časovni razvoj kvantnega stanja (vendar naj opozorimo, da tega ne moremo povezovati z metuljevim učinkom v klasičnih kaotičnih sistemih). Delci se prerazporedijo in preidejo v nov zastoj, toda novo kvantno stanje se povsod v prostoru močno razlikuje od tistega pred meritvijo. To je presenetljivo, saj običajno pričakujemo, da majhne motnje v fizikalnih sistemih izzvenijo. Zamislite si padec majhnega kamna v jezero: na vodni površini sproži valove, ki se razpršijo in sčasoma izginejo. Podobno bi pričakovali, da bodo kvantni sistemi sčasoma »pozabili« meritve na posameznih delcih, vendar pa se v našem modelu s kinetičnimi vezmi to ne zgodi. Valovi, ki jih v takem modelu sproži kvantna meritev, namreč nikoli ne izginejo.
Tako vedenje nekaterih modelov s kinetičnimi vezmi sta izkoristila Saverio Bocini in Maurizio Fagotti, fizika z Univerze Pariz-Saclay. Razvila sta metodo, pri kateri z natančno izbrano meritvijo enega samega delca sprožimo dinamiko, ki vodi v večdelčno prepleteno stanje. Njuna metoda sloni na matematični lastnosti, da je vsota kvantnih stanj spet kvantno stanje. Če ne vemo točno, v kakšnem kvantnem stanju so delci, potem to zapišemo kot vsoto različnih možnih stanj – svojo negotovost torej matematično zakodiramo kot vsoto možnosti. Bocini in Fagotti sta našla preprosto meritev, po kateri delci z verjetnostjo 50 % ostanejo v zastoju, z verjetnostjo 50 % pa jih kvantna dinamika s kinetičnimi vezmi sčasoma dramatično prerazporedi kot pri metuljevem učinku. Negotovost je sedaj zakodirana kot vsota dveh stanj, ki sta zelo različni povsod v prostoru. Takim stanjem velikokrat pravimo Schrödingerjeva mačka. Izkaže se, da gre za stanja z največjo možno mero prepletenosti, ki so zelo pomembna v kvantni komunikaciji in šifriranju. Poimenovanje Schrödingerjeva mačka izvira iz miselnega poskusa, ki si ga je zamislil Erwin Schrödinger, eden izmed očetov kvantne mehanike, da bi ponazoril njeno neintuitivno naravo. Predstavljajmo si mačko, ki je ujeta v škatli s smrtonosno pastjo. Dokler ne odpremo škatle in preverimo, ali je mačka sprožila past, ne vemo, ali je živa ali mrtva. To negotovost zapišemo kot vsoto dveh kvantnih stanj: stanja, v katerem je mačka živa, ter tistega, v katerem je mrtva. Verjetno se vsi strinjamo, da sta ti dve stanji zelo različni.
Spontan razvoj maksimalno prepletenih kvantnih stanj (kot so Schrödingerjeve mačke) bi lahko imel široke posledice. Eden izmed kvantnih sistemov, ki ga danes uporabljajo za testiranje delovanja kvantnih računalnikov, se namreč obnaša kot model s kinetičnimi vezmi: v njem bi lahko delovala zgoraj opisana metoda, pri kateri se Schrödingerjeva mačka razvije iz meritve na enem izmed delcev. To pa pomeni, da bi lahko nekoč spontan razvoj večdelčnih prepletenih stanj uporabili v kvantnih računalnikih. Seveda moramo biti pri napovedih uporabnosti previdni, saj simulacija omenjenega modela za testiranje kvantnih računalnikov zahteva namensko programiranje kvantnega računalnika. Priprava prepletenih stanj na tak način zato ni zares spontana. Vendar pa poznamo vrsto materialov, ki jih ta model precej natančno opiše. S pomočjo sintetiziranja teh materialov bi se lahko nekoč izognili programirani pripravi kvantnih stanj. Zato lahko z optimizmom zremo v prihodnost, v kateri bomo priča rojstvu Schrödingerjeve mačke (maksimalno prepletenega kvantnega stanja) in rešitvi problemov, ki so za klasične računalnike pretežki.